Objectives
- Determine if a relation, equation, or graph defines a function using the definition as well as the vertical line test.
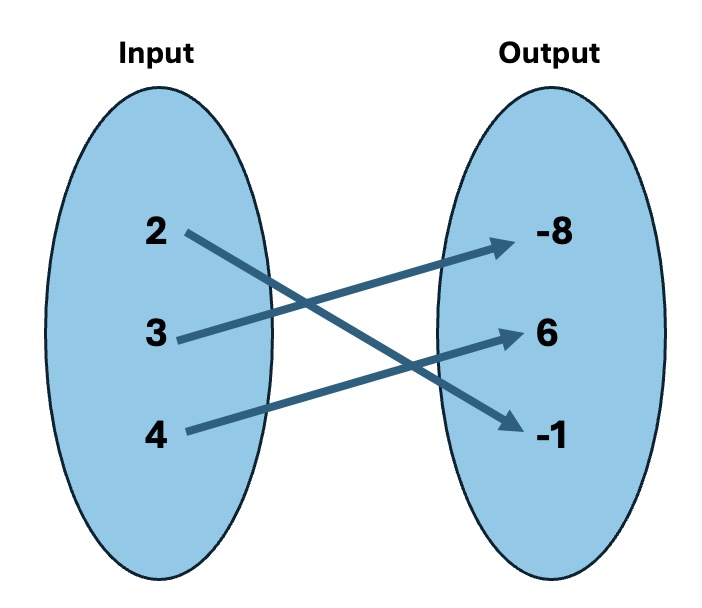
| \(x\) | \(y\) |
|---|---|
| \(-5\) | \(-2\) |
| \(-4\) | \(-5\) |
| \(-2\) | \(8\) |
| \(8\) | \(-4\) |
| \(8\) | \(1\) |

| \(x\) | \(y\) |
|---|---|
| \(-2\) | \(5\) |
| \(0\) | \(4\) |
| \(3\) | \(6\) |
| \(8\) | \(1\) |
https://tbil.org/precalculus/preview/exercises/#/bank/FN1/.