Skip to main content

Section 2.7 Differentiating implicitly defined functions (DF7)

Observation 2.7.1.

Many of the equations that has been discussed so far fall under the category of an explicit equation. An explicit equation is one in which the relationship between \(x\) and \(y\) is given explicitly, such as \(y = f(x)\text{.}\) In this section we will examine when the relationship between \(x\) and \(y\) is given implicity. An implicit equation looks like \(f(x,y) = g(x,y)\) where both sides of the equation may depend on both \(x\) and \(y\text{.}\)

Observation 2.7.2.

Note that if we are taking the derivative of \(f(x)\) with respect to \(x\text{,}\) then
\begin{equation*} \frac{d}{dx}(f(x)) = f'(x). \end{equation*}
However, if we are taking the derivative of \(g(y(x))\) with respect to \(x\text{,}\) then
\begin{equation*} \frac{d}{dx}(g(y)) = g'(y) \cdot \frac{dy}{dx}. \end{equation*}

Activity 2.7.3.

For this activity we want to find the equation of a tangent line for a circle with radius 5 centered at the origin, \(x^2+y^2 = 25,\) at the point \((-3,-4).\)

(a)

The derivative with respect to \(x\) for the equation of the circle is given by which expression.

  1. \(\displaystyle 2x + 2y\frac{dy}{dx} = 25\)

  2. \(\displaystyle 2x + y\frac{dy}{dx} = 0\)

  3. \(\displaystyle 2x + 2y\frac{dy}{dx} = 0\)

  4. \(\displaystyle 2x + 2\frac{dy}{dx} = 25\)

(b)

Solving for \(\frac{dy}{dx}\) gives?

  1. \(\displaystyle \frac{dy}{dx} = \frac{25-2x}{2y}\)

  2. \(\displaystyle \frac{dy}{dx} = -\frac{2x}{y}\)

  3. \(\displaystyle \frac{dy}{dx} = -\frac{x}{y}\)

  4. \(\displaystyle \frac{dy}{dx} = \frac{25-2x}{2}\)

(c)

Plug the point \((-3,-4)\) into the expression found above for the derivative to get the slope of the tangent line.

(d)

Use the value for the slope of the tangent line to obtain the equation of the tangent line.

Activity 2.7.4.

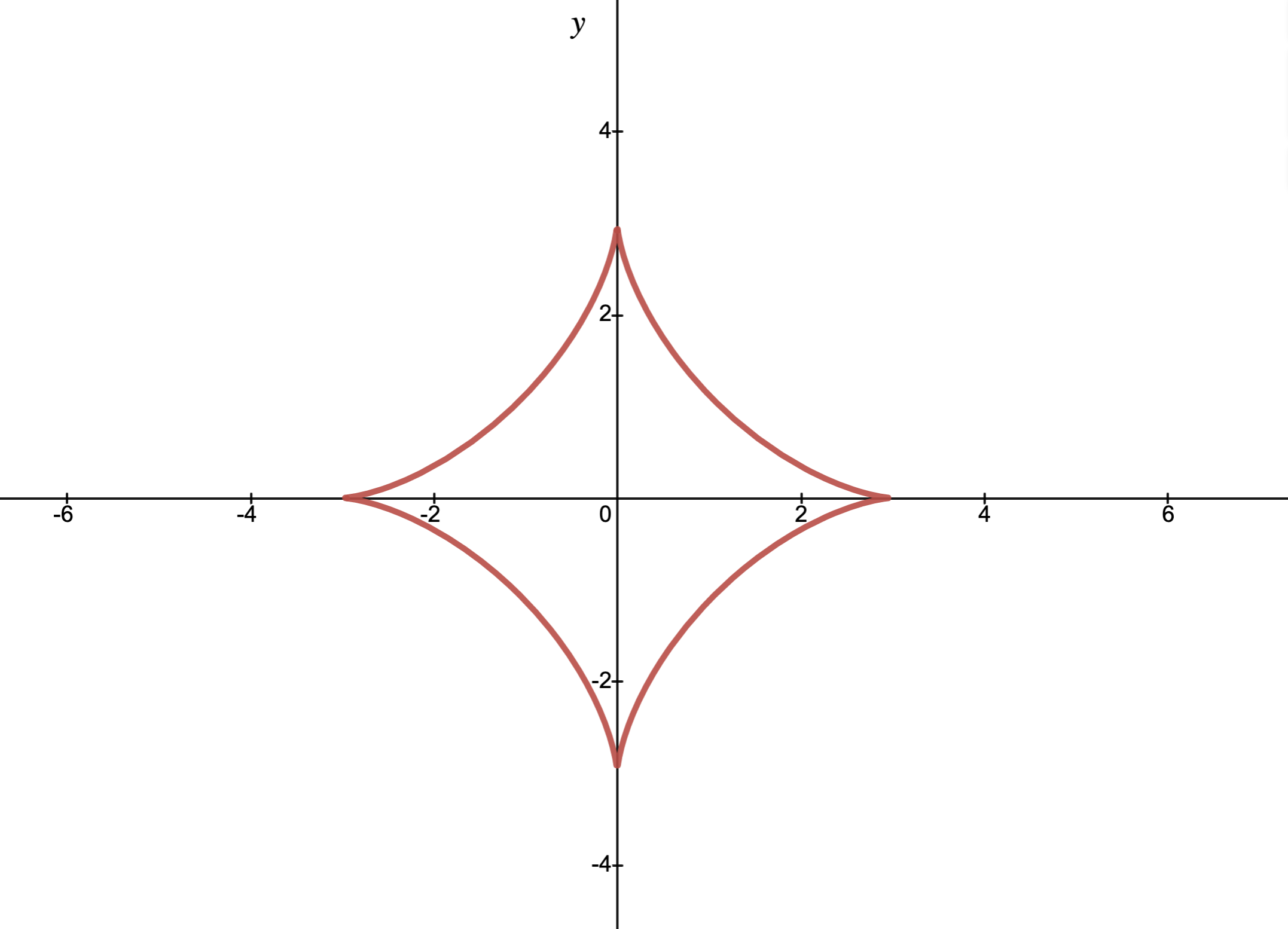
The curve given in Figure 38 is an example of an astroid. The equation of this astroid is \(x^{2/3} + y^{2/3} = 3^{2/3}\text{.}\) What is the derivative with respect \(x\) for this astroid? (Solve for \(\frac{dy}{dx}\)).

Figure 38. Graph of \(x^{2/3} + y^{2/3} = 3^{2/3}\text{.}\)

  1. \(\displaystyle \frac{dy}{dx} = \frac{x^{-1/3}}{y^{-1/3}}\)

  2. \(\displaystyle \frac{dy}{dx} = \frac{y^{-1/3}}{x^{-1/3}}\)

  3. \(\displaystyle \frac{dy}{dx} = \frac{3^{-1/3}-x^{-1/3}}{y^{-1/3}}\)

  4. \(\displaystyle \frac{dy}{dx} = -\frac{x^{-1/3}}{y^{-1/3}}\)

Activity 2.7.5.

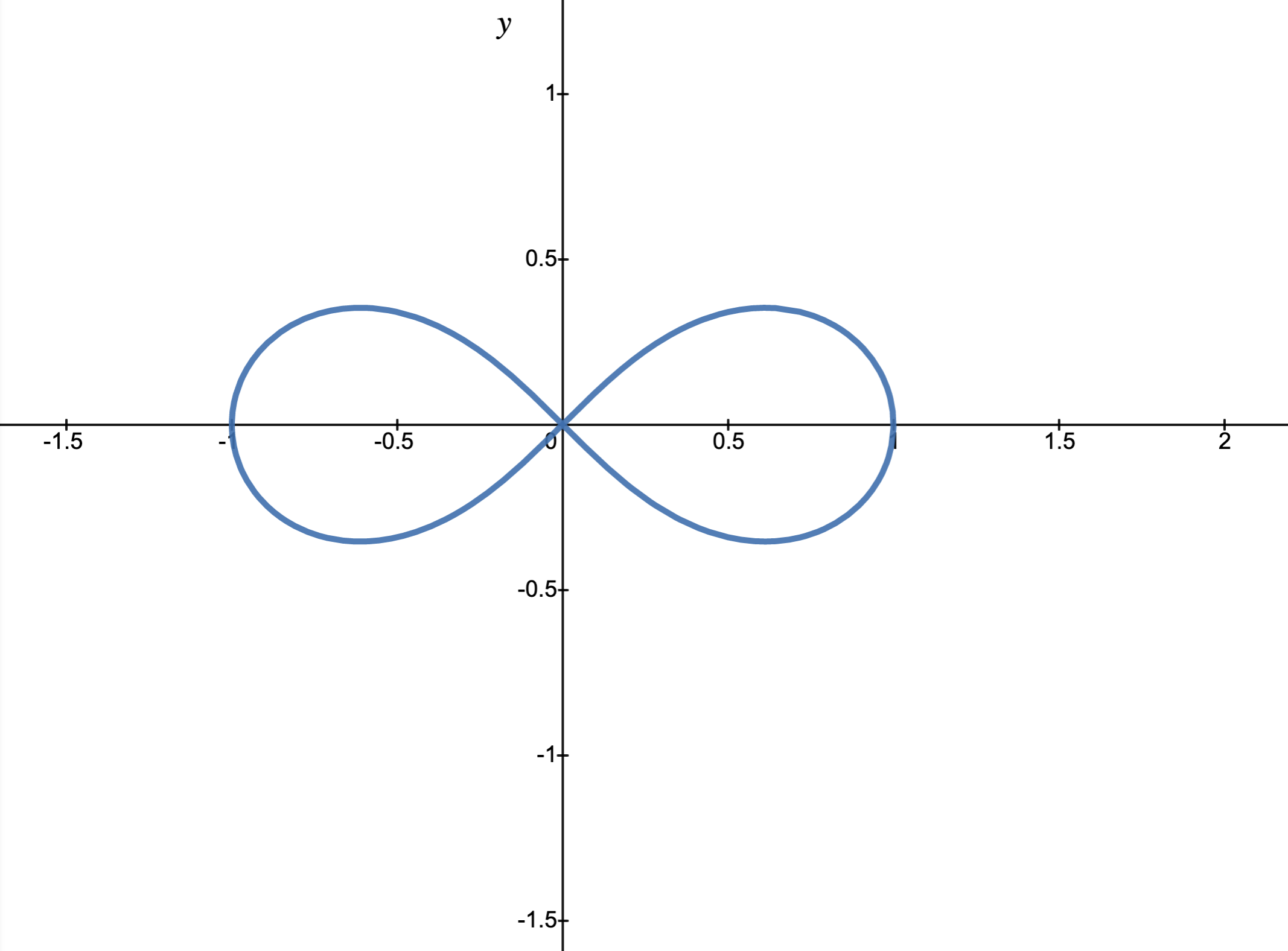
An example of a lemniscate is given in Figure 39. The equation of this lemniscate is \((x^{2} + y^{2})^2 = x^2 - y^2\text{.}\) What is the derivative with respect \(x\) for this lemniscate? (Solve for \(\frac{dy}{dx}\)).

Figure 39. Graph of \((x^{2} + y^{2})^2 = x^2 - y^2\text{.}\)

  1. \(\displaystyle \frac{dy}{dx} = \frac{x(1-2(x^2+y^2))}{y+2(x^2+y^2)}\)

  2. \(\displaystyle \frac{dy}{dx} = \frac{x(1-2(x^2+y^2))}{y(1+2(x^2+y^2))}\)

  3. \(\displaystyle \frac{dy}{dx} = \frac{y(1+2(x^2+y^2))}{x(1-2(x^2+y^2))}\)

  4. \(\displaystyle \frac{dy}{dx} = \frac{y+2(x^2+y^2)}{x(1-2(x^2+y^2))}\)

Activity 2.7.6.

Explain how to use implicit differentiation to find \(\frac{dy}{dx}\) for each of the following equations.

(a)

\begin{equation*} -5 \, x^{5} - 5 \, \cos\left(y\right) = 3 \, y^{4} + 2 \end{equation*}

(b)

\begin{equation*} -5 \, y e^{x} + 5 \, \sin\left(x\right) = 0 \end{equation*}

Activity 2.7.7.

To take the derivative of some explicit equations you might need to make it an implicit equation. For this activity we will find the derivative of \(y = x^x\text{.}\) Make the equation an implicit equation by taking natural logarithm of both sides, this gives \(\ln(y) = x\ln(x)\text{.}\) Knowing this, what is \(\frac{dy}{dx}\text{?}\) This process to find a derivative is known as logarithmic differentiation.

  1. \(\displaystyle \frac{dy}{dx} = x^x(\ln(x) + 1)\)

  2. \(\displaystyle \frac{dy}{dx} = \frac{(\ln(x)+1)}{x^x}\)

  3. \(\displaystyle \frac{dy}{dx} = x^x(\ln(x) + x)\)

  4. \(\displaystyle \frac{dy}{dx} = \frac{(\ln(x)+x)}{x^x}\)

Activity 2.7.8.

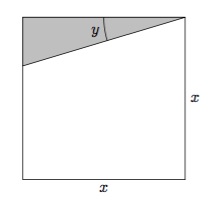
Valerie is building a square chicken coop with side length \(x\text{.}\) Because she needs a separate place for the rooster, she needs to put fence around the square and also along the diagonal line shown. The fence costs $20 per linear meter, and she has a budget of $900.
Figure 40. A diagram of the chicken coop.

(a)

Which of the following equations gives the relationship between \(x\) and \(y\text{?}\) Make sure you can explain why!

  1. \(\displaystyle 20x + \frac{80x}{\cos(y)}=900\)

  2. \(\displaystyle 80x + \frac{20x}{\cos(y)}=900\)

  3. \(\displaystyle 80x + \frac{20x}{\sin(y)}=900\)

  4. \(\displaystyle 20x + \frac{80x}{\sin(y)}=900\)

(b)

If Valerie builds the coop with \(y=\pi/3\) (and wants to use her whole budget), find what side length \(x\) she needs to use.

(c)

Find the slope of the curve at this point and interpret what this value tells Valerie.