Section 4.5 FTC for definite integrals (IN5)
Learning Outcomes
Evaluate a definite integral using the Fundamental Theorem of Calculus.
Activity 4.5.1.
Find the area beteween \(f(x)=\frac{1}{2}x+2\) and the \(x\)-axis from \(x=2\) to \(x=6\text{.}\)
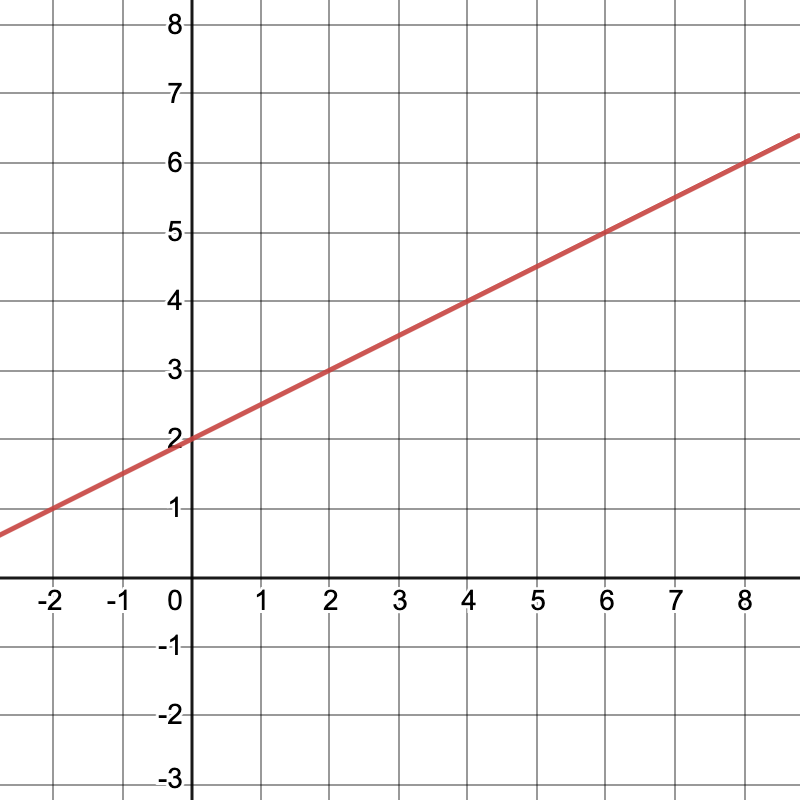
Activity 4.5.2.
Approximate the area under the curve \(f(x)=(x-1)^2+2\) on the interval \([1,5]\) using a left Riemann sum with four uniform subdivisions. Draw your rectangles on the graph.
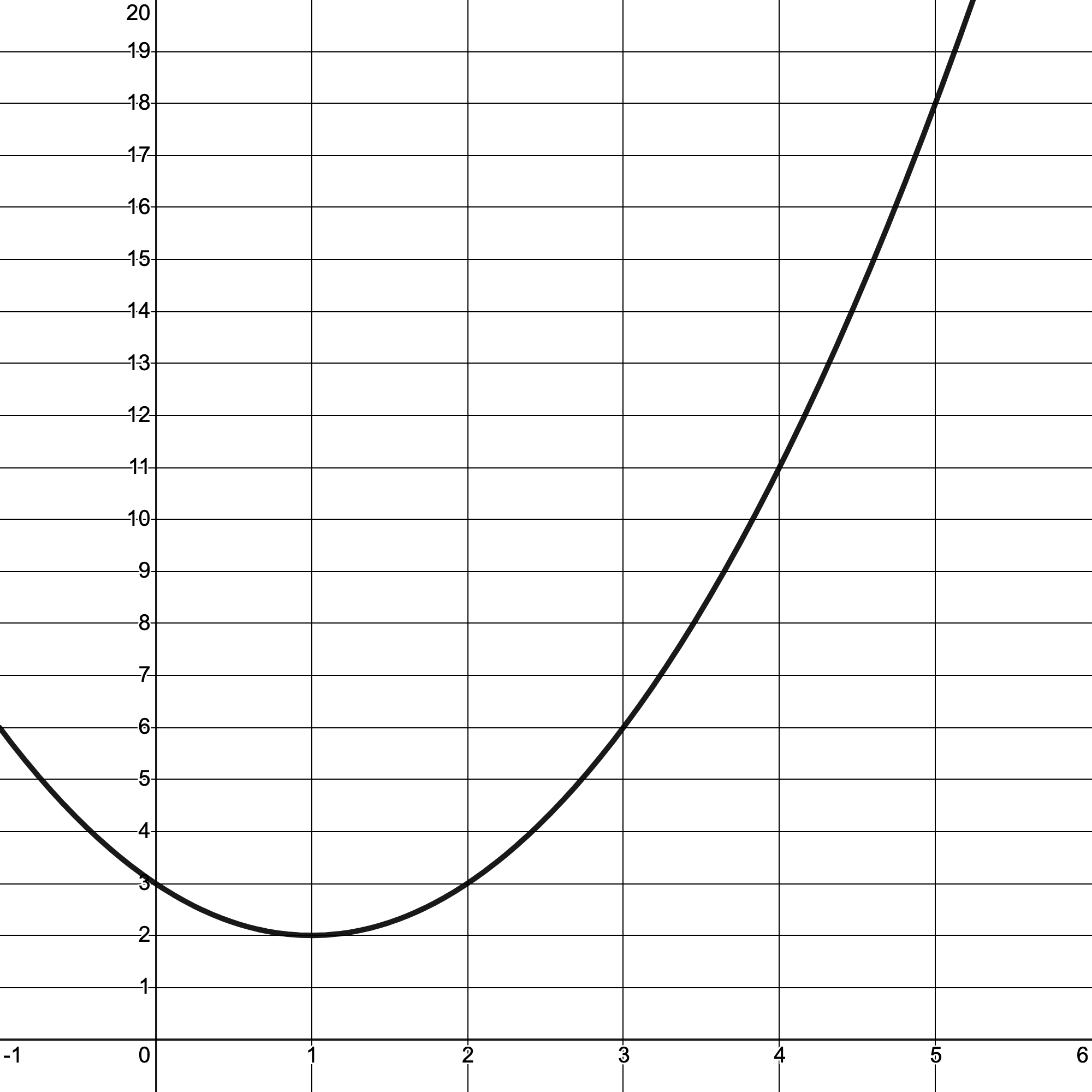
Definition 4.5.3.
Let \(f(x)\) be a continuous function on the interval \([a,b]\text{.}\) Divide the interval into \(n\) subdivisions of equal width, \(\Delta x\text{,}\) and choose a point \(x_i\) in each interval. Then, the definite integral of \(f(x)\) from \(a\) to \(b\) is
Activity 4.5.4.
How does \(\displaystyle \int_2^6 \left(\frac{1}{2}x+2\right) \, dx\) relate to Activity 4.5.1? Could you use Activity 4.5.1 to find \(\displaystyle \int_0^4 \left(\frac{1}{2}x+2\right) \, dx\text{?}\) What about \(\displaystyle \int_1^7 \left(\frac{1}{2}x+2\right) \, dx\text{?}\)
Remark 4.5.5. Properties of Definite Integrals.
If \(f\) is defined at \(x=a\text{,}\) then \(\displaystyle \int_a^a f(x) \, dx =0\text{.}\)
If \(f\) is integrable on \([a,b]\text{,}\) then \(\displaystyle \int_a^b f(x) \, dx = - \displaystyle \int_b^a f(x) \, dx\text{.}\)
If \(f\) is integrable on \([a,b]\) and \(c\) is in \([a,b]\text{,}\) then \(\displaystyle \int_a^b f(x) \, dx = \displaystyle \int_a^c f(x) \, dx + \displaystyle \int_c^b f(x) \, dx\text{.}\)
If \(f\) is integrable on \([a,b]\) and \(k\) is a constant, then \(kf\) is integrable on \([a,b]\) and \(\displaystyle \int_a^b kf(x) \, dx = k\displaystyle \int_a^b f(x) \, dx\text{.}\)
If \(f\) and \(g\) are integrable on \([a,b]\text{,}\) then \(f\pm g\) are integrable on \([a,b]\) and \(\displaystyle \int_a^b [f(x) \pm g(x)] \, dx =\displaystyle \int_a^b f(x) \, dx \pm \displaystyle \int_a^b g(x) \, dx\text{.}\)
Activity 4.5.6.
Suppose that \(\displaystyle\int_1^5 f(x)\, dx = 10\) and \(\displaystyle\int_5^7 f(x)\, dx = 4 \text{.}\)Find each of the following.
(a)
\(\displaystyle\int_1^7 f(x)\, dx \)
(b)
\(\displaystyle\int_5^1 f(x)\, dx \)
(c)
\(\displaystyle\int_7^7 f(x)\, dx \)
(d)
\(3 \displaystyle\int_5^7 f(x)\, dx \)
Observation 4.5.7.
We've been looking at two big things in this chapter: antiderivatives and the area under a curve. In the early days of the development of calculus, they were not known to be connected to one another. The integral sign wasn't originally used in both instances. (Gottfried Leibniz introduced it as an elongated S to represent the sum when finding the area.) Connecting these two seemingly separate problems is done by the Fundamental Theorem of Calculus
Theorem 4.5.8. The Fundamental Theorem of Calculus.
If a function \(f\) is continuous on the closed interval \([a,b]\) and \(F\) is an antiderivative of \(f\) on the interval \([a,b]\text{,}\) then
Activity 4.5.9.
Evaluate the following definite integrals. Include a sketch of the graph with the area you've found shaded in. Approximate the area to check to see if your definite integral answer makes sense. (Note: Just a guess, you don't have to use Riemann sums. Use the grid to help.)
(a)
\(\displaystyle \int_0^2 \left(x^2+3\right) \, dx \)
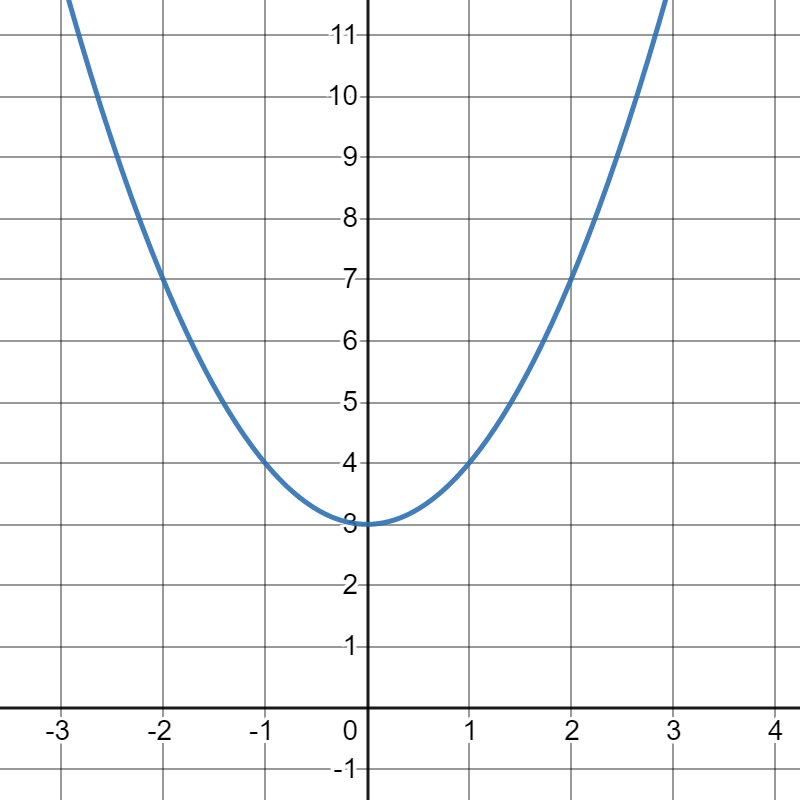
(b)
\(\displaystyle \int_1^9 \left(\sqrt{x}\right) \, dx \)
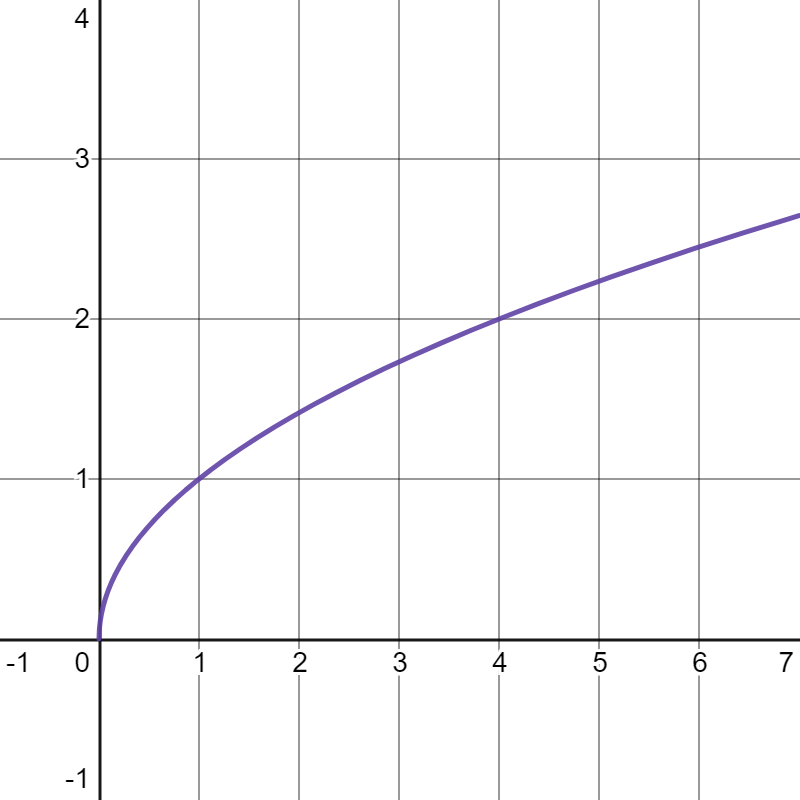
(c)
\(\displaystyle \int_{-\pi/4}^{\pi/2} \left(\cos x\right) \, dx \)
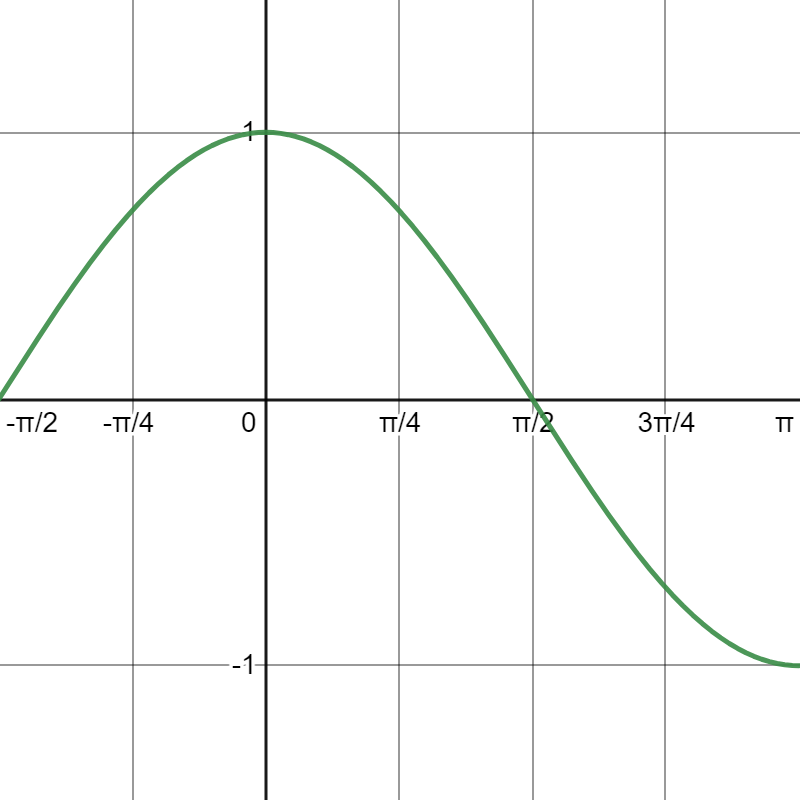
Activity 4.5.10.
Find the area between \(f(x)=2x-6 \) on the interval \([0,8]\) using
geometry
the definite integral
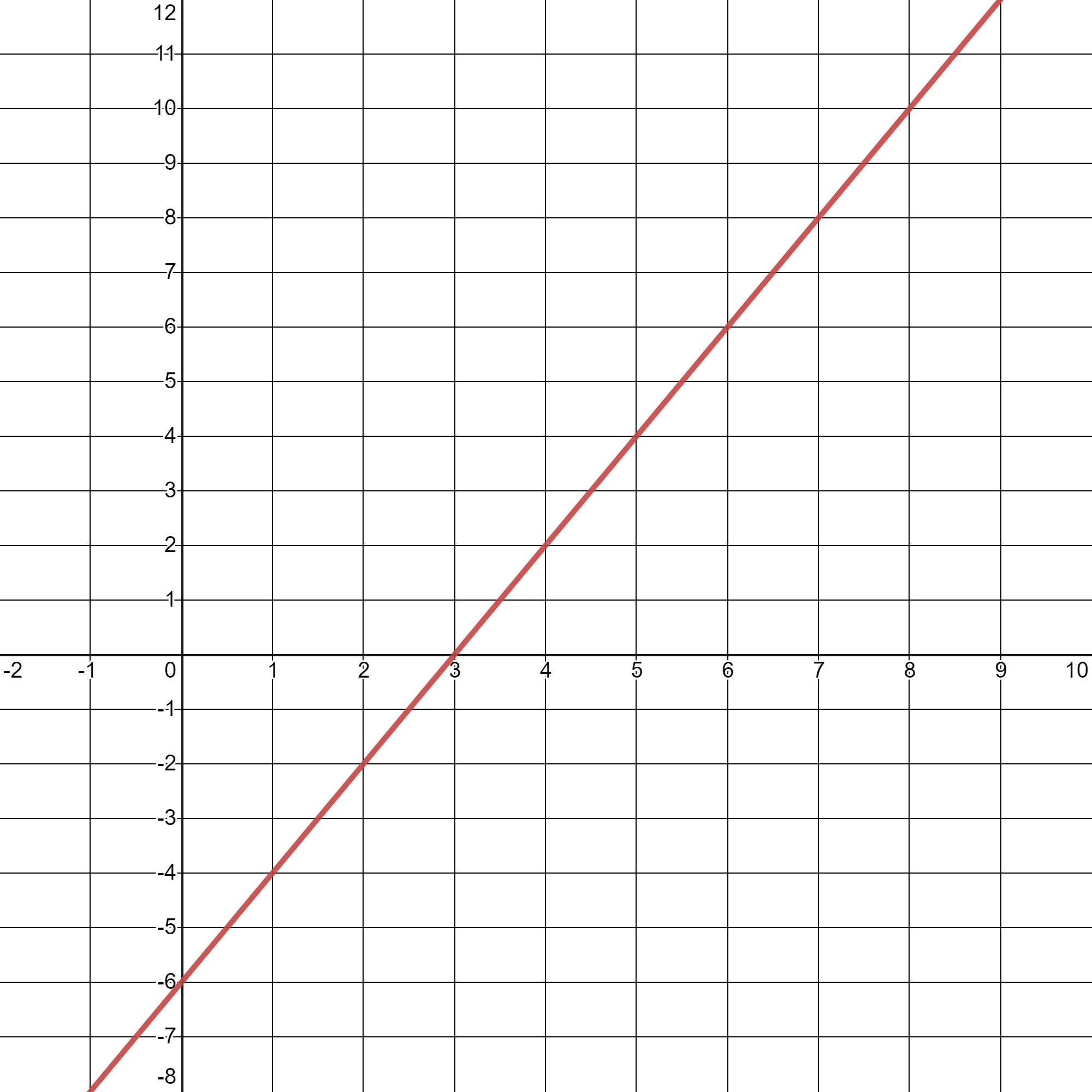
What do you notice?
Activity 4.5.11.
Find the area bounded by the curves \(f(x)=e^x-2\text{,}\) the \(x\)-axis, \(x=0\text{,}\) and \(x=1\text{.}\)
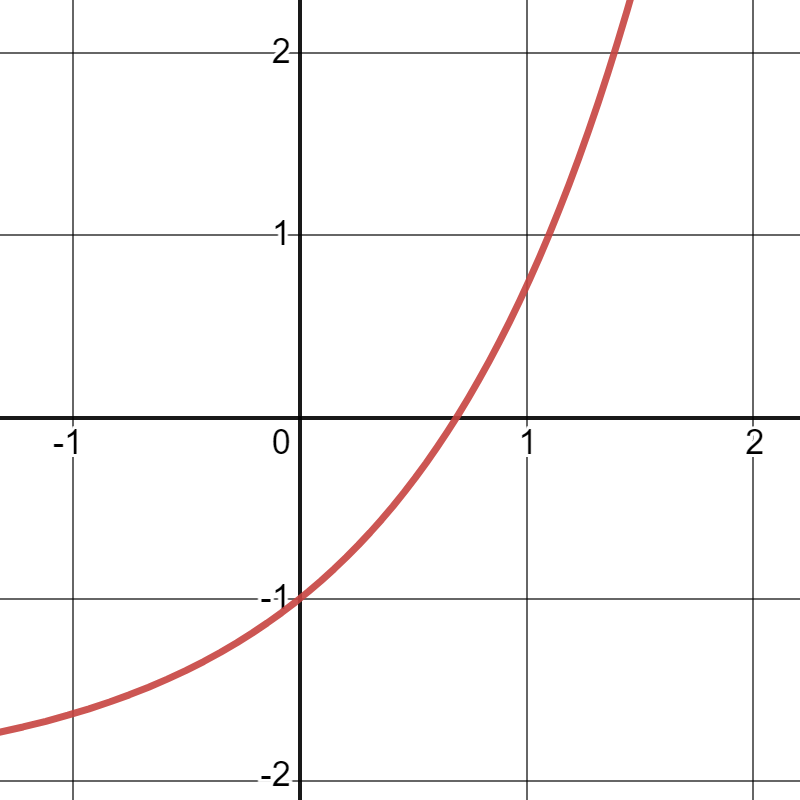
Activity 4.5.12.
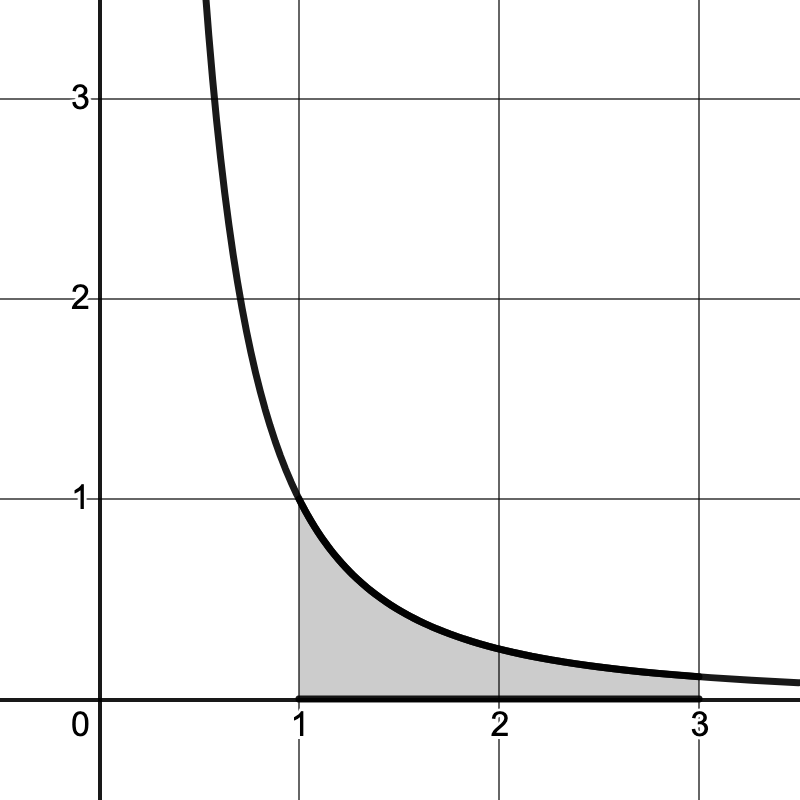
Set up a definite integral that represents the shaded area. Then find the area of the given region using the definite integral.
(a)
\(y=\frac{1}{x^2}\)
(b)
\(y=3x^2-x^3\)
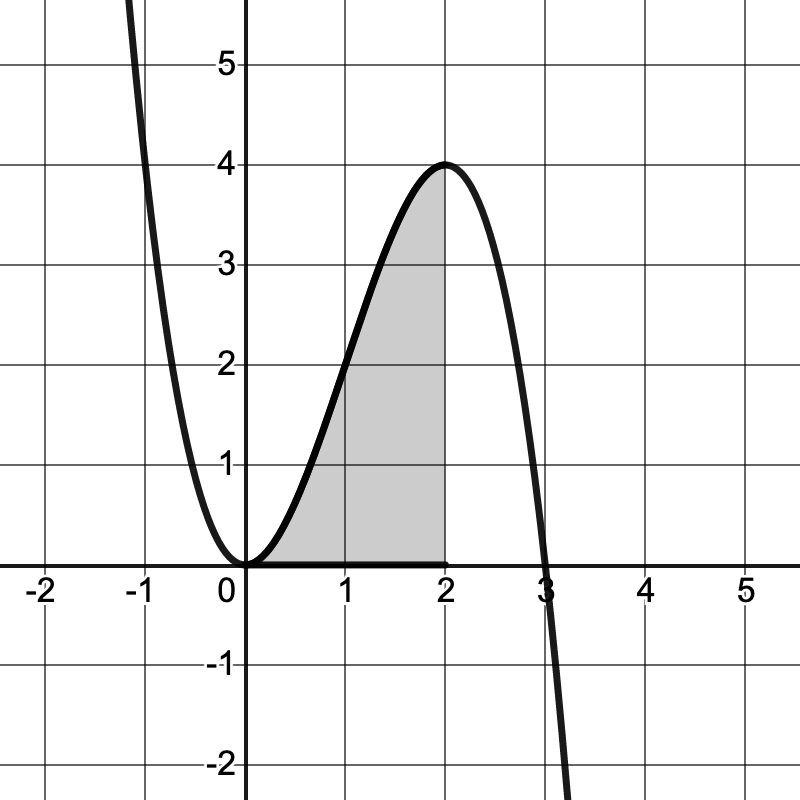
Activity 4.5.13.
Explain how to compute the exact value of each of the following definite integrals using the Fundamental Theorem of Calculus. Leave all answers in exact form, with no decimal approximations.