Section 4.8 Area between curves (IN8)
Learning Outcomes
Use definite integral(s) to compute the area bounded by several curves.
Remark 4.8.1.
In Section 4.7, we learned how to find the area between a curve and the \(x\)-axis (\(f(x)=0\)) using a definite integral. What if we want the area between any two functions? What if the \(x\)-axis is not one of the boundaries?
In this section, we'll investigate how a definite integral may be used to represent the area between two curves.
Activity 4.8.2.
Consider the functions given by \(f(x) = 5-(x-1)^2\) and \(g(x) = 4-x\text{.}\)
(a)
Use algebra to find the points where the graphs of \(f\) and \(g\) intersect.
(b)
Sketch an accurate graph of \(f\) and \(g\) on the \(xy\) plane, labeling the curves by name and the intersection points with ordered pairs.
(c)
Find and evaluate exactly an integral expression that represents the area between \(y = f(x)\) and the \(x\)-axis on the interval between the intersection points of \(f\) and \(g\text{.}\) Shade this area in your sketch.
(d)
Find and evaluate exactly an integral expression that represents the area between \(y = g(x)\) and the \(x\)-axis on the interval between the intersection points of \(f\) and \(g\text{.}\) Shade this area in your sketch.
(e)
Let's denote the area between \(y = f(x)\) and the \(x\)-axis as \(A_f\) and the area between \(y = g(x)\) and the \(x\)-axis as \(A_g\text{.}\) How could we use \(A_f\) and \(A_g\) to find exact area between \(f\) and \(g\) between their intersection points?
We could find \(A_f + A_g\) to find the area between the curves.
We could find \(A_f - A_g\) to find the area between the curves.
We could find \(A_g - A_f\) to find the area between the curves.
Note 4.8.3.
We've seen from Activity 4.8.2 that a natural way to think about the area between two curve is as the area beneath the upper curve minus the area beneath the lower curve.
Activity 4.8.4.
We now look for a general way of writing definite integrals for the area between two given curves, \(f(x)\) and \(g(x)\text{.}\) Consider this area, illustrated in Figure 73.
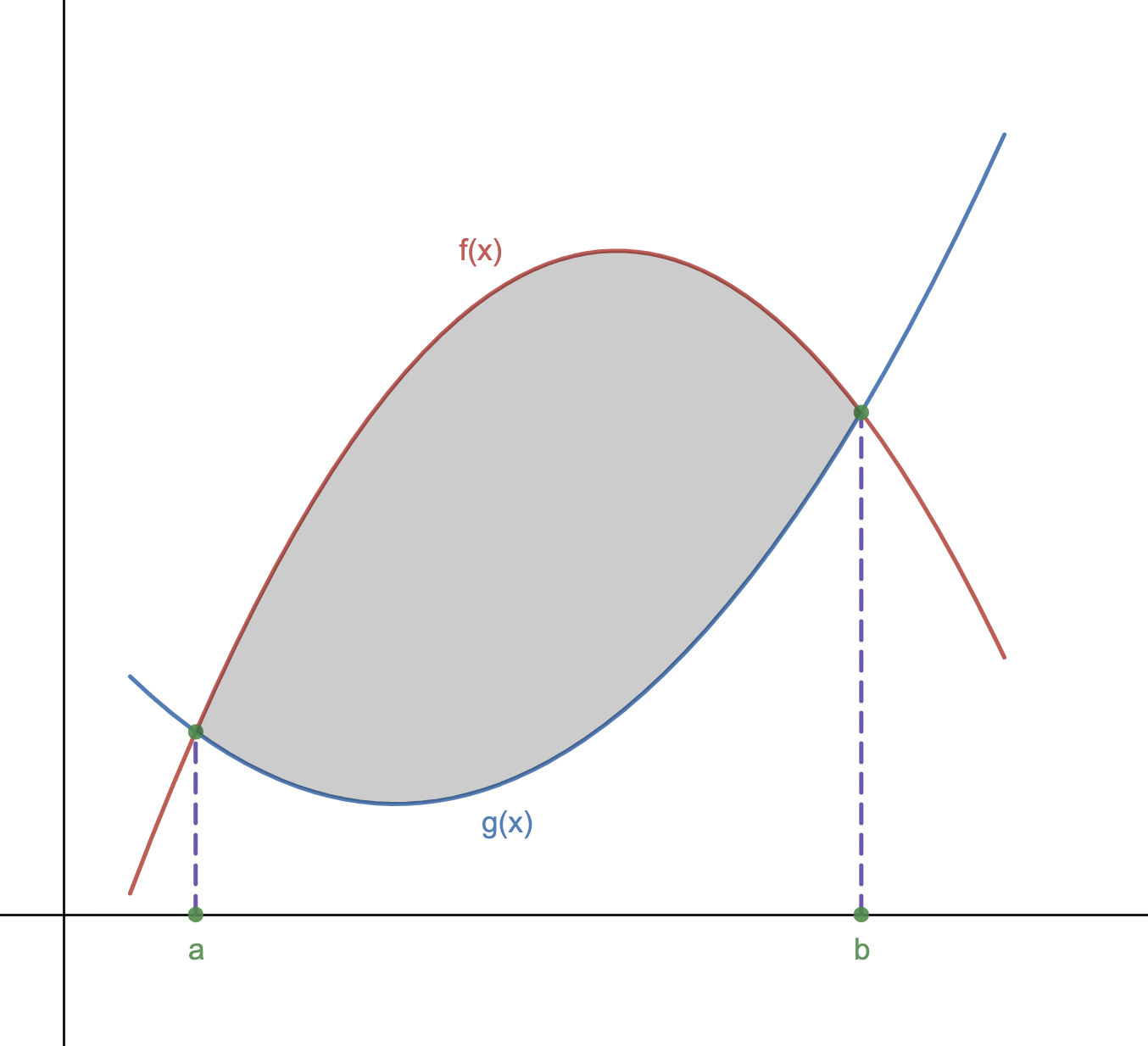
(a)
How could we represent the shaded area in Figure 73?
\(\displaystyle \int_b^a f(x) \,dx - \int_b^a g(x) \,dx\)
\(\displaystyle \int_a^b f(x) \,dx - \int_a^b g(x) \,dx\)
\(\displaystyle \int_b^a g(x) \,dx - \int_b^a f(x) \,dx\)
\(\displaystyle \int_a^b g(x) \,dx - \int_a^b f(x) \,dx\)
(b)
The two definite integrals above can be rewritten as one definite integral using the sum and difference property of definite integrals:
If \(f\) and \(g\) are continuous functions, then
Use the property above to represent the shaded area in Figure 73 using one definite integral.
\(\displaystyle \int_b^a (f(x) - g(x)) \,dx\)
\(\displaystyle \int_a^b (f(x) - g(x)) \,dx\)
\(\displaystyle \int_b^a (g(x) - f(x)) \,dx\)
\(\displaystyle \int_a^b (g(x) - f(x)) \,dx\)
Fact 4.8.5.
If two curves \(y = f(x)\) and \(y = g(x)\) intersect at \((a,g(a))\) and \((b,g(b))\text{,}\) and for all \(x\) such that \(a \le x \le b\text{,}\) \(f(x) \ge g(x)\text{,}\) then the area between the curves is \(A = \int_a^b (f(x) - g(x)) \, dx\text{.}\)
Activity 4.8.6.
In each of the following problems, our goal is to determine the area of the region described. For each region, (i) determine the intersection points of the curves, (ii) sketch the region whose area is being found, (iii) draw and label a representative slice, and (iv) state the area of the representative slice. Then, state a definite integral whose value is the exact area of the region, and evaluate the integral to find the numeric value of the region's area.
(a)
The finite region bounded by \(y = \sqrt{x}\) and \(y = \frac{1}{4}x\text{.}\)
(b)
The finite region bounded by \(y = 12-2x^2\) and \(y = x^2 - 8\text{.}\)
(c)
The area bounded by the \(y\)-axis, \(f(x) = \cos(x)\text{,}\) and \(g(x) = \sin(x)\text{,}\) where we consider the region formed by the first positive value of \(x\) for which \(f\) and \(g\) intersect.
(d)
The finite regions between the curves \(y = x^3-x\) and \(y = x^2\text{.}\)
Activity 4.8.7.
Let \(\mathbf{R}\) be the finite region bounded by the graphs of \(y={\left(x + 5\right)}^{2} - 1\) and \(y=7 \, x + 34\text{.}\)
Sketch an illustration of \(\mathbf R\text{,}\) and then explain how to express the area of \(\mathbf R\) in the following two ways:(Do not evaluate either definite integral.)
As a definite integral with respect to \(x\text{.}\)
As a definite integral with respect to \(y\text{.}\)